Instructions
Please download lab materials lab04.zip from our QQ group if you don't have one.
In this lab, you have one task: Complete the required problems described in section 3 and submit your code to our OJ website.
The starter code for these problems is provided in lab04.py.
Submission: As instructed before, you need to submit your work with Ok by python ok --submit.
You may submit more than once before the deadline,
and your score of this assignment will be the highest one of all your submissions.
Readings: You might find the following reference to the textbook useful:
Review
Consult this section if you need a refresher on the material for this lab. It's okay to skip directly to the next section and refer back here when you get stuck.
Data Abstraction
Data abstraction is a powerful concept in computer science that allows programmers to treat code as objects -- for example, car objects, chair objects, people objects, etc. That way, programmers don't have to worry about the detail of code/implementation -- we just have to know what it does.
Data abstraction mimics how we think about the world. When you want to drive a car, you don't need to know how the engine was built or what kind of material the tires are made of. You just have to know how to turn the wheel and press the gas pedal.
An abstract data type(ADT for short) consists of two types of functions:
- Constructors: functions that build the abstract data type.
- Selectors: functions that retrieve information from the data type.
Programmers design ADTs to abstract away how information is stored and calculated such that the end users do not need to know how constructors and selectors are implemented. The nature of abstract data types allows users to assume that the functions have been written correctly and work as described.
List
Lists are Python data structures that can store multiple elements. Each element can be any type and can even be another list! A list is written as a comma separated list of expressions within square brackets:
>>> list_of_nums = [1, 2, 3, 4]
>>> list_of_bools = [True, True, False, False]
>>> nested_lists = [1, [2, 3], [4, [5]]]
Each element in a list has an index. Lists are zero-indexed, meaning their indices start at 0 and increase in sequential order. To retrieve an element from a list, we can use list indexing:
>>> lst = [6, 5, 4, 3, 2, 1]
>>> lst[0]
6
>>> lst[3]
3
Often times we need to know how long a list is when we're working with it. To find the length of a list, we can call the function len on it:
>>> len([])
0
>>> len([2, 4, 6, 8, 10])
5
Tip: Recall that empty lists, [], are falsy values. Therefore, you can use an if statement like the following if you only want to do operations on non-empty lists:
if lst: # Do stuff with the elements of listThis is equivalent to:
if len(lst) > 0: # Do stuff
You can also create a copy of a portion of the list using list slicing.
To slice a list, use the syntax: lst[<start index>:<end index>].
This expression evaluates to a new list containing the elements of lst
starting at and including the element at <start index> up to
the element at <end index>.
>>> lst = [True, False, True, True, False]
>>> lst[1:4]
[False, True, True]
>>> lst[:3] # Start index defaults to 0
[True, False, True]
>>> lst[3:] # End index defaults to len(lst)
[True, False]
>>> lst[:] # Creates a copy of the whole list
[True, False, True, True, False]
List Comprehensions
List comprehension is a compact and powerful way of creating new lists out of sequences. The general syntax for a list comprehension is the following:
[<expression> for <element> in <sequence> if <conditional>]
The syntax is designed to read like English: "Compute the expression for each element in the sequence if the conditional is true for that element."
Let's see it in action:
>>> [i**2 for i in [1, 2, 3, 4] if i % 2 == 0]
[4, 16]
Here, for each element i in [1, 2, 3, 4] that satisfies the condition i % 2 == 0,
we evaluate the expression i**2 and insert the resulting values into a new list.
In other words, this list comprehension will create a new list that
contains the square of each of the even elements of the original list.
If we were to write the example above using a for statement, it would look like:
>>> lst = []
>>> for i in [1, 2, 3, 4]:
... if i % 2 == 0:
... lst = lst + [i**2]
>>> lst
[4, 16]
Note: The if clause in a list comprehension is optional. For example, we can just write:
>>> [i**2 for i in [1, 2, 3, 4]] [1, 4, 9, 16]
Tree
A tree is a data structure that represents a hierarchy of information.
A file system is a good example of a tree structure.
For example, within your NJU-SICP folder, you have folders separating your projects,
lab assignments, and homework.
The next level is folders that separate different assignments,
hw01, lab01, hog, etc., and inside those are the files themselves,
including the code directory where the starter files are placed.
Below is an incomplete diagram of what your NJU-SICP directory might look like:
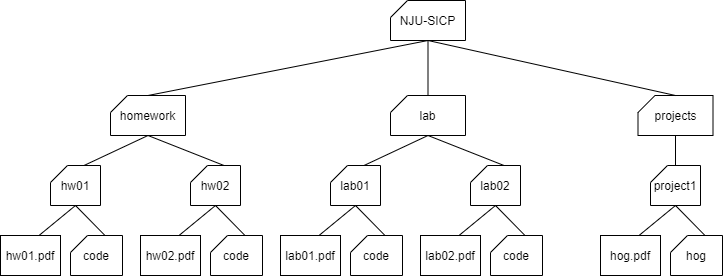
As you can see, unlike trees in the nature, the root of a tree ADT is starting at the top and the leaves are placed at the bottom.
Some terminologies about trees:
- root: the node at the top of the tree
- label: the value in a node, selected by the label function
- branches: a list of trees directly under the tree's root, selected by the branches function
- leaf: a tree with zero branches
- node: any location within the tree (e.g., root node, leaf nodes, etc.)
Our tree ADT consists of a root and a list of its branches. To create a tree and access its root and branches, we can use the following constructor and selectors:
- Constructor
tree(label, branches=[]): creates a tree object with the givenlabelvalue at its root node and list ofbranches. Notice that the second argument to this constructor,branches, is optional - if you want to make a tree with no branches, leave this argument empty.
- Selectors
label(tree): returns the value in the root node of tree.branches(tree): returns the list of branches of the given tree.
- Convenience function
is_leaf(tree): returnsTrueiftree's list ofbranchesis empty, andFalseotherwise.
For example, the tree generated by the following Python code:
number_tree = tree(1,
[tree(2),
tree(3,
[tree(4),
tree(5)]),
tree(6,
[tree(7)])])
would look like this:
1
/ | \
2 3 6
/ \ \
4 5 7
To extract the number 3 from this tree,
which is the label of the root of its second branch, we can do this by:
label(branches(number_tree)[1])
The print_tree function prints out a tree in a human-readable form.
The exact form follows the pattern illustrated above, where the root is unindented,
and each of its branches is indented by one level further.
def print_tree(t, indent=0):
"""Print a representation of this tree in which each node is
indented by two spaces times its depth from the root.
>>> print_tree(tree(1))
1
>>> print_tree(tree(1, [tree(2)]))
1
2
>>> numbers = tree(1, [tree(2), tree(3, [tree(4), tree(5)]), tree(6, [tree(7)])])
>>> print_tree(numbers)
1
2
3
4
5
6
7
"""
print(' ' * indent + str(label(t)))
for b in branches(t):
print_tree(b, indent + 1)
Mutability
We say that an object is mutable if its state can change as code is executed. The process of changing an object's state is called mutation. Examples of mutable objects include lists and dictionaries. Examples of objects that are not mutable include tuples and functions.
We have seen how to use the == operator to check if two expressions evaluate to the same values.
We now introduce a new comparison operator, is, that checks if two expressions evaluate to the same identities.
Wait, what's the difference? For primitive values, there is no difference:
>>> 2 + 2 == 3 + 1
True
>>> 2 + 2 is 3 + 1
True
This is because all primitives have the same identity under the hood. However, with non-primitive values, such as lists and large numbers, each object has its own identity. That means you can construct two objects that may look exactly the same but have different identities.
>>> large_num1 = 23333333333333333333
>>> large_num2 = 23333333333333333333
>>> large_num1 == large_num2
True
>>> large_num1 is large_num2
False
>>> lst1 = [1, 2, 3, 4]
>>> lst2 = [1, 2, 3, 4]
>>> lst1 == lst2
True
>>> lst1 is lst2
False
Here, although the lists referred by lst1 and lst2 have the same contents, they are not the same object. In other words, they are the same in terms of equality, but not in terms of identity.
This is important in the discussion of mutability because when we mutate an object, we simply change its state, not its identity.
>>> lst1 = [1, 2, 3, 4]
>>> lst2 = lst1
>>> lst1.append(5)
>>> lst2
[1, 2, 3, 4, 5]
>>> lst1 is lst2
True
You may think of the name in Python as the pointer variable in the C language, and the identity of an object in Python as the address of an object in the C language. In such an analogy:
- assigning an object to a name is similar to assigning the address of this object to a pointer variable,
- the
==operator compares whether the two pointed values are the same,- and
isoperator compares whether the two pointers are the same.
You can use the built-in function id to fetch the identity of an object,
which differs during different runnings of the Python interpreter.
In fact, the expression a is b is equivalent to id(a) == id(b).
>>> lst = [1, 2, 3, 4]
>>> id(lst)
2624875298056 # It's different on your machine
>>> lst.append(5)
>>> id(lst)
2624875298056
Required Problems
In this section, you are required to complete the problems below and submit your code to OJ website as instructed in lab00 to get your answer scored.
Problem 1: Mobiles (400pts)
Acknowledgements:
This mobile example is based on a classic problem from Structure and Interpretation of Computer Programs, Section 2.2.2.
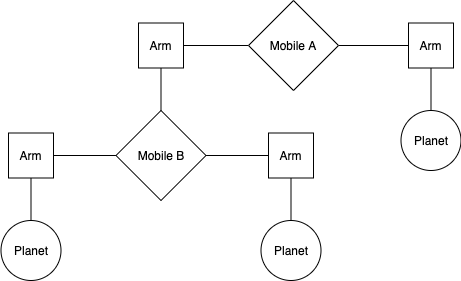
We are making a planetarium mobile. A mobile is a type of hanging sculpture. A binary mobile consists of two arms. Each arm is a rod of a certain length, from which hangs either a planet or another mobile.
We will represent a binary mobile using the data abstractions below:
- A mobile has a left arm and a right arm.
- An arm has a positive length and something hanging at the end, either a mobile or planet.
- A planet has a positive size.
Problem 1.1 Weights
Implement the planet data abstraction by completing the planet constructor and the size selector
so that a planet is represented using a two-element list where the first element is the string 'planet' and the second element is its size.
The total_weight example is provided to demonstrate use of the mobile, arm, and planet abstractions.
# The constructor and selectors of the planet
def planet(size):
"""Construct a planet of some size.
>>> planet(5)
['planet', 5]
"""
assert size > 0
"*** YOUR CODE HERE ***"
def size(w):
"""Select the size of a planet.
>>> p = planet(5)
>>> size(p)
5
"""
assert is_planet(w), 'must call size on a planet'
"*** YOUR CODE HERE ***"
def is_planet(w):
"""Whether w is a planet."""
return type(w) == list and len(w) == 2 and w[0] == 'planet'
# examples and usage
def examples():
t = mobile(arm(1, planet(2)),
arm(2, planet(1)))
u = mobile(arm(5, planet(1)),
arm(1, mobile(arm(2, planet(3)),
arm(3, planet(2)))))
v = mobile(arm(4, t), arm(2, u))
return (t, u, v)
def total_weight(m):
"""Return the total weight of m, a planet or mobile.
>>> t, u, v = examples()
>>> total_weight(t)
3
>>> total_weight(u)
6
>>> total_weight(v)
9
"""
if is_planet(m):
return size(m)
else:
assert is_mobile(m), "must get total weight of a mobile or a planet"
return total_weight(end(left(m))) + total_weight(end(right(m)))
Note: the code listed above is the part you should fill in for the lab, see lab04.py for the complete codes.
Problem 1.2: Balanced(100pts)
Hint: for more information on this problem (with more pictures!), please refer to this document.
Implement the balanced function, which returns whether m is a balanced mobile.
A mobile is balanced if two conditions are both met:
- The torque applied by its left arm is equal to that applied by its right arm. Torque of the left arm is the length of the left rod multiplied by the total weight hanging from that rod. Likewise for the right.
- Each of the mobiles hanging at the end of its arms is balanced.
Planets themselves are balanced.
def balanced(m):
"""Return whether m is balanced.
>>> t, u, v = examples()
>>> balanced(t)
True
>>> balanced(v)
True
>>> w = mobile(arm(3, t), arm(2, u))
>>> balanced(w)
False
>>> balanced(mobile(arm(1, v), arm(1, w)))
False
>>> balanced(mobile(arm(1, w), arm(1, v)))
False
"""
assert is_mobile(m)
"*** YOUR CODE HERE ***"
Problem 1.3: Mobile to Tree(200pts)
Implement totals_tree, which takes a mobile (or planet) and returns a tree whose root is the total weight of the input.
For a planet, the result should be a leaf.
For a mobile, the result should be a tree and its branches should be
the totals_tree for each ends of the arms.
from ADT import tree, label, branches, is_leaf, print_tree
def totals_tree(m):
"""Return a tree representing the mobile/planet with its total weight at the root.
>>> t, u, v = examples()
>>> print_tree(totals_tree(t))
3
2
1
>>> print_tree(totals_tree(u))
6
1
5
3
2
>>> print_tree(totals_tree(v))
9
3
2
1
6
1
5
3
2
"""
assert is_mobile(m) or is_planet(m)
"*** YOUR CODE HERE ***"
Hint: you may want to use some helper functions imported from ADT.py.
Problem 2: Preorder (100pts)
Define the function preorder, which takes in a tree as an argument and
returns a list of all the entries in the tree in the order that print_tree would print them.
The following diagram shows the order that the nodes would get printed, with the arrows representing function calls.
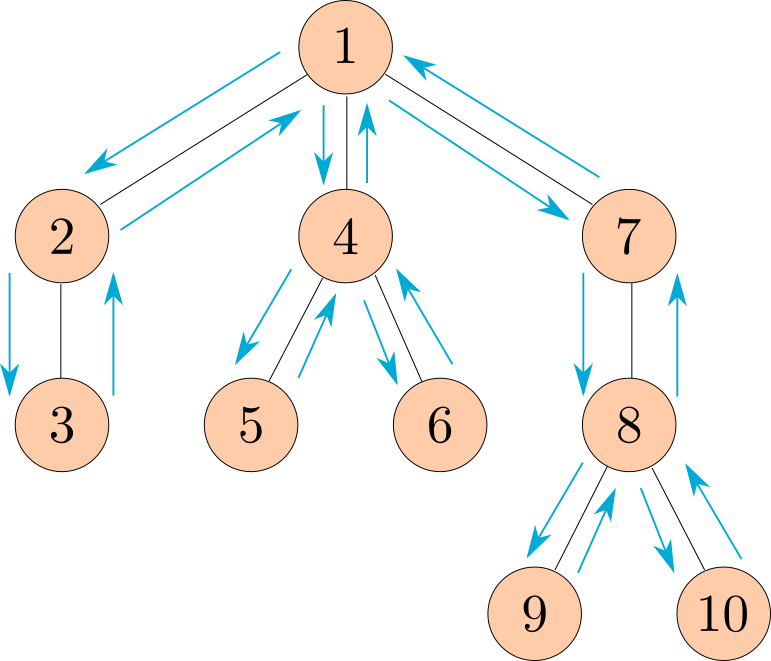
Note: This ordering of the nodes in a tree is called a preorder traversal.
def preorder(t):
"""Return a list of the entries in this tree in the order that they
would be visited by a preorder traversal (see problem description).
>>> numbers = tree(1, [tree(2), tree(3, [tree(4), tree(5)]), tree(6, [tree(7)])])
>>> preorder(numbers)
[1, 2, 3, 4, 5, 6, 7]
>>> preorder(tree(2, [tree(4, [tree(6)])]))
[2, 4, 6]
"""
"*** YOUR CODE HERE ***"
Problem 3: Trie (200pts)
Write a function has_path that takes in a tree t and a string word.
It returns True if there is a path starting from the root,
along which the entries spell out the word. Otherwise, it returns False.
(This data structure is called a trie, and it has a lot of cool applications!---think autocomplete).
You may assume that every node's label is exactly one character.
def has_path(t, word):
"""Return whether there is a path in a tree where the entries along the path
spell out a particular word.
>>> greetings = tree('h', [tree('i'),
... tree('e', [tree('l', [tree('l', [tree('o')])]),
... tree('y')])])
>>> print_tree(greetings)
h
i
e
l
l
o
y
>>> has_path(greetings, 'h')
True
>>> has_path(greetings, 'i')
False
>>> has_path(greetings, 'hi')
True
>>> has_path(greetings, 'hello')
True
>>> has_path(greetings, 'hey')
True
>>> has_path(greetings, 'bye')
False
"""
assert len(word) > 0, 'no path for empty word.'
"*** YOUR CODE HERE ***"
Problem 4: Insert (100pts)
Write a function insert_items which takes as input a list lst, an argument entry, and another argument elem.
This function will check through each item present in lst to see if it is equivalent with entry.
Upon finding an equivalent entry, the function should modify the list by placing elem into the list right after the found entry.
At the ending of the function, the modified list should be returned.
See the doctests for examples about the usage of this function. Use list mutation to modify the original list, no new lists should be created or returned.
Be careful in situations where the values passed into entry and elem are equivalent, so as not to create an infinitely long list while iterating through it. If you find that your code is taking more than a few seconds to run, it is most likely that the function is in a loop of inserting new values.
def insert_items(lst, entry, elem):
"""
>>> test_lst = [1, 5, 8, 5, 2, 3]
>>> new_lst = insert_items(test_lst, 5, 7)
>>> new_lst
[1, 5, 7, 8, 5, 7, 2, 3]
>>> large_lst = [1, 4, 8]
>>> large_lst2 = insert_items(large_lst, 4, 4)
>>> large_lst2
[1, 4, 4, 8]
>>> large_lst3 = insert_items(large_lst2, 4, 6)
>>> large_lst3
[1, 4, 6, 4, 6, 8]
>>> large_lst3 is large_lst
True
"""
"*** YOUR CODE HERE ***"
Hint: You may use the
lst.insert(ind, obj)to insert an element obj to a position indexed by ind. Search the internet for more information about its usage. Here is just a reference from Python Documentation.