Tree
A tree is a data structure that represents a hierarchy of information.
A file system is a good example of a tree structure.
For example, within your NJU-SICP folder, you have folders separating your projects,
lab assignments, and homework.
The next level is folders that separate different assignments,
hw01, lab01, hog, etc., and inside those are the files themselves,
including the code directory where the starter files are placed.
Below is an incomplete diagram of what your NJU-SICP directory might look like:
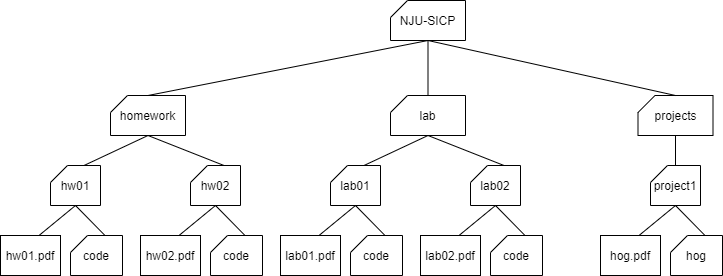
As you can see, unlike trees in the nature, the root of a tree ADT is starting at the top and the leaves are placed at the bottom.
Some terminologies about trees:
- root: the node at the top of the tree
- label: the value in a node, selected by the label function
- branches: a list of trees directly under the tree's root, selected by the branches function
- leaf: a tree with zero branches
- node: any location within the tree (e.g., root node, leaf nodes, etc.)
Our tree ADT consists of a root and a list of its branches. To create a tree and access its root and branches, we can use the following constructor and selectors:
- Constructor
tree(label, branches=[]): creates a tree object with the givenlabelvalue at its root node and list ofbranches. Notice that the second argument to this constructor,branches, is optional - if you want to make a tree with no branches, leave this argument empty.
- Selectors
label(tree): returns the value in the root node of tree.branches(tree): returns the list of branches of the given tree.
- Convenience function
is_leaf(tree): returnsTrueiftree's list ofbranchesis empty, andFalseotherwise.
For example, the tree generated by the following Python code:
number_tree = tree(1,
[tree(2),
tree(3,
[tree(4),
tree(5)]),
tree(6,
[tree(7)])])
would look like this:
1
/ | \
2 3 6
/ \ \
4 5 7
To extract the number 3 from this tree,
which is the label of the root of its second branch, we can do this by:
label(branches(number_tree)[1])
The print_tree function prints out a tree in a human-readable form.
The exact form follows the pattern illustrated above, where the root is unindented,
and each of its branches is indented by one level further.
def print_tree(t, indent=0):
"""Print a representation of this tree in which each node is
indented by two spaces times its depth from the root.
>>> print_tree(tree(1))
1
>>> print_tree(tree(1, [tree(2)]))
1
2
>>> numbers = tree(1, [tree(2), tree(3, [tree(4), tree(5)]), tree(6, [tree(7)])])
>>> print_tree(numbers)
1
2
3
4
5
6
7
"""
print(' ' * indent + str(label(t)))
for b in branches(t):
print_tree(b, indent + 1)