2.2 Tree Recursion

A tree recursive function is a recursive function that makes more than one call to itself, resulting in a tree-like series of calls.

A classic example of a tree recursion function is finding the nth Fibonacci number:

def fib(n):
    if n == 0 or n == 1:
        return n
    return fib(n - 1) + fib(n - 2)

Calling fib(6) results in the following call structure (where f is fib):

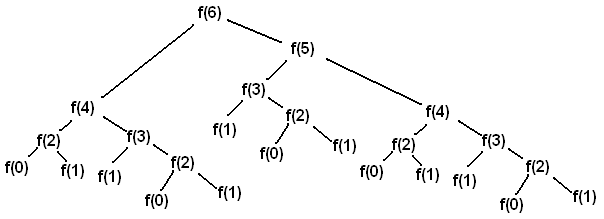
Each f(i) node represents a recursive call to fib. Each recursive call makes another two recursive calls. f(0) and f(1) do not make any recursive calls because they are the base cases of the function. Because of these base cases, we are able to terminate the recursion and beginning accumulating the values.

Generally, tree recursion is effective when you want to explore multiple possibilities or choices at a single step. In these types of problems, you make a recursive call for each choice or for a group of choices. Here are some examples:

• Given a list of paid tasks and a limited amount of time, which tasks should you choose to maximize your pay? This is actually a variation of the Knapsack problem, which focuses on finding some optimal combination of different items.
• Suppose you are lost in a maze and see several different paths. How do you find your way out? This is an example of path finding, and is tree recursive because at every step, you could have multiple directions to choose from that could lead out of the maze.
• Your dryer costs $2 per cycle and accepts all types of coins. How many different combinations of coins can you create to run the dryer? This is similar to the partitions problem from the textbook.