Instructions
Please download lab materials lab08.zip from our QQ group if you don't have one.
In this lab, you have two tasks:
- Think about what would Scheme display in section 3 and verify your answer with Ok.
- Complete the required problems described in section 4 and submit your code to our OJ website.
The starter code for these problems is provided in lab08.scm.
Submission: As instructed before, you need to submit your work with Ok by python ok --submit.
You may submit more than once before the deadline,
and your score of this assignment will be the highest one of all your submissions.
Readings: You might find the following references to the textbook useful:
Review
Consult this section if you need a refresher on the material for this lab. It's okay to skip directly to the next section and refer back here when you get stuck.
Scheme
Scheme is a famous functional programming language from the 1970s. It is a dialect of Lisp (which stands for LISt Processing). The first observation most people make is the unique syntax, which uses a prefix notation and (often many) nested parentheses (see http://xkcd.com/297/). Scheme features first-class functions and optimized tail-recursion, which were relatively new features at the time.
Our course uses a custom version of Scheme (which you will build for Project 4) included in the starter ZIP archive. To start the interpreter, type
python scheme. To run a Scheme program interactively, typepython scheme -i <file.scm>. To exit the Scheme interpreter, type(exit). You may find it useful to try code.cs61a.org/scheme when working through problems, as it can draw environment and box-and-pointer diagrams and it lets you walk your code step-by-step (similar to Python Tutor). Don't forget to submit your code through Ok though!
Expressions
Primitive Expressions
Just like in Python, atomic, or primitive, expressions in Scheme take a single step to evaluate. These include numbers, booleans, symbols.
Note that ; starts a comment in Scheme, just like # in Python.
scm> 1234 ; integer
1234
scm> 123.4 ; real number
123.4
Symbols
Out of these, the symbol type is the only one we didn't encounter in Python. A symbol acts a lot like a Python name, but not exactly. Specifically, a symbol in Scheme is also a type of value. On the other hand, in Python, names only serve as expressions; a Python expression can never evaluate to a name.
scm> quotient ; A name bound to a built-in procedure
#[quotient]
scm> 'quotient ; An expression that evaluates to a symbol
quotient
scm> 'hello-world!
hello-world!
Booleans
In Scheme, all values except the special boolean value #f are interpreted as true values (unlike Python, where there are some false-y values like 0). Our particular version of the Scheme interpreter allows you to write True and False in place of #t and #f. This is not standard.
scm> #t
#t
scm> True
#t
scm> #f
#f
scm> False
#f
Call Expressions
Like Python, the operator in a Scheme call expression comes before all the operands. Unlike Python, the operator is included within the parentheses and the operands are separated by spaces rather than with commas. However, evaluation of a Scheme call expression follows the exact same rules as in Python:
- Evaluate the operator. It should evaluate to a procedure.
- Evaluate the operands, left to right.
- Apply the procedure to the evaluated operands.
Here are some examples using built-in procedures:
scm> (+ 1 2)
3
scm> (- 10 (/ 6 2))
7
scm> (modulo 35 4)
3
scm> (even? (quotient 45 2))
#t
Special Forms
The operator of a special form expression is a special form. What makes a special form "special" is that they do not follow the three rules of evaluation stated in the previous section. Instead, each special form follows its own special rules for execution, such as short-circuiting before evaluating all the operands.
Some examples of special forms that we'll study today are the if, cond, define, and lambda forms. Read their corresponding sections below to find out what their rules of evaluation are!
Control Structures
if Expressions
The if special form allows us to evaluate one of two expressions based on a predicate. It takes in two required arguments and an optional third argument:
(if <predicate> <if-true> [if-false])
The first operand is what's known as a predicate expression in Scheme, an expression whose value is interpreted as either #t or #f.
The rules for evaluating an if special form expression are as follows:
- Evaluate
<predicate>. - If
<predicate>evaluates to a truth-y value, evaluate and return the value if the expression<if-true>. Otherwise, evaluate and return the value of[if-false]if it is provided.
Can you see why this expression is a special form? Compare the rules between a regular call expression and an if expression. What is the difference?
Step 2 of evaluating call expressions requires evaluating all of the operands in order. However, an
ifexpression will only evaluate two of its operands, the conditional expression and either<true-result>or<false-result>. Because we don't evaluate all the operands in anifexpression, it is a special form.
Let's compare a Scheme if expression with a Python if statement:
| Scheme | Python |
|---|---|
|
|
Although the code may look the same, what happens when each block of code is evaluated is actually very different. Specifically, the Scheme expression, given that it is an expression, evaluates to some value. However, the Python if statement simply directs the flow of the program.
Another difference between the two is that it's possible to add more lines of code into the suites of the Python if statement, while a Scheme if expression expects just a single expression for each of the true result and the false result.
One final difference is that in Scheme, you cannot write elif cases. If you want to have multiple cases using the if expression, you would need multiple branched if expressions:
| Scheme | Python |
|---|---|
|
|
cond Expressions
Using nested if expressions doesn't seem like a very practical way to take care of multiple cases. Instead, we can use the cond special form, a general conditional expression similar to a multi-clause if/elif/else conditional expression in Python. cond takes in an arbitrary number of arguments known as clauses. A clause is written as a list containing two expressions: (<p> <e>).
(cond
(<p1> <e1>)
(<p2> <e2>)
...
(<pn> <en>)
[(else <else-expression>)])
The first expression in each clause is a predicate. The second expression in the clause is the return expression corresponding to its predicate. The optional else clause has no predicate.
The rules of evaluation are as follows:
- Evaluate the predicates
<p1>,<p2>, ...,<pn>in order until you reach one that evaluates to a truth-y value. - If you reach a predicate that evaluates to a truth-y value, evaluate and return the corresponding expression in the clause.
- If none of the predicates are truth-y and there is an
elseclause, evaluate and return<else-expression>.
As you can see, cond is a special form because it does not evaluate its operands in their entirety; the predicates are evaluated separately from their corresponding return expression. In addition, the expression short circuits upon reaching the first predicate that evaluates to a truth-y value, leaving the remaining predicates unevaluated.
The following code is roughly equivalent (see the explanation in the if expression section):
| Scheme | Python |
|---|---|
|
|
Lists
As you read through this section, it may be difficult to understand the differences between the various representations of Scheme containers. We recommend that you use CS61A's online Scheme interpreter to see the box-and-pointer diagrams of pairs and lists that you're having a hard time visualizing! (Use the command
(autodraw)to toggle the automatic drawing of diagrams.)
Lists
Scheme lists are very similar to the linked lists we've been working with in Python. Just like how a linked list is constructed of a series of Link objects, a Scheme list is constructed with a series of pairs, which are created with the constructor cons.
Scheme lists require that the cdr is either another list or nil, an empty list. A list is displayed in the interpreter as a sequence of values (similar to the __str__ representation of a Link object). For example,
scm> (cons 1 (cons 2 (cons 3 nil)))
(1 2 3)
Here, we've ensured that the second argument of each cons expression is another cons expression or nil.

We can retrieve values from our list with the car and cdr procedures, which now work similarly to the Python Link's first and rest attributes. (Curious about where these weird names come from? Check out their etymology.)
scm> (define a (cons 1 (cons 2 (cons 3 nil)))) ; Assign the list to the name a
a
scm> a
(1 2 3)
scm> (car a)
1
scm> (cdr a)
(2 3)
scm> (car (cdr (cdr a)))
3
If you do not pass in a pair or nil as the second argument to cons, it will not create a proper list:
scm> (cons 1 2) ; (1 . 2) represents a list end with 2
(1 . 2)
list Procedure
There are a few other ways to create lists. The list procedure takes in an arbitrary number of arguments and constructs a list with the values of these arguments:
scm> (list 1 2 3)
(1 2 3)
scm> (list 1 (list 2 3) 4)
(1 (2 3) 4)
scm> (list (cons 1 (cons 2 nil)) 3 4)
((1 2) 3 4)
Note that all of the operands in this expression are evaluated before being put into the resulting list.
Quote Form
We can also use the quote form to create a list, which will construct the exact list that is given. Unlike with the list procedure, the argument to ' is not evaluated.
scm> '(1 2 3)
(1 2 3)
scm> '(cons 1 2) ; Argument to quote is not evaluated
(cons 1 2)
scm> '(1 (2 3 4))
(1 (2 3 4))
Built-In Procedures for Lists
There are a few other built-in procedures in Scheme that are used for lists. Try them out in the interpreter!
scm> (null? nil) ; Checks if a value is the empty list
#t
scm> (append '(1 2 3) '(4 5 6)) ; Concatenates two lists
(1 2 3 4 5 6)
scm> (length '(1 2 3 4 5)) ; Returns the number of elements in a list
5
Defining Names
The special form define is used to define variables and functions in Scheme. There are two versions of the define special form. To define variables, we use the define form with the following syntax:
(define <name> <expression>)
The rules to evaluate this expression are
- Evaluate the
<expression>. - Bind its value to the
<name>in the current frame. - Return
<name>.
The second version of define is used to define procedures:
(define (<name> <param1> <param2> ...) <body> )
To evaluate this expression:
- Create a lambda procedure with the given parameters and
<body>. - Bind the procedure to the
<name>in the current frame. - Return
<name>.
The following two expressions are equivalent:
scm> (define foo (lambda (x y) (+ x y)))
foo
scm> (define (foo x y) (+ x y))
foo
define is a special form because its operands are not evaluated at all! For example, <body> is not evaluated when a procedure is defined, but rather when it is called. <name> and the parameter names are all names that should not be evaluated when executing this define expression.
Lambda Functions
All Scheme procedures are lambda procedures. To create a lambda procedure, we can use the lambda special form:
(lambda (<param1> <param2> ...) <body>)
This expression will create and return a function with the given parameters and body, but it will not alter the current environment. This is very similar to a lambda expression in Python!
scm> (lambda (x y) (+ x y)) ; Returns a lambda function, but doesn't assign it to a name
(lambda (x y) (+ x y))
scm> ((lambda (x y) (+ x y)) 3 4) ; Create and call a lambda function in one line
7
A procedure may take in any number of parameters. The <body> may contain multiple expressions. There is not an equivalent version of a Python return statement in Scheme. The function will simply return the value of the last expression in the body.
What Would Scheme Display?
Let's familiarize ourselves with some built-in Scheme procedures and special forms!
Use Ok to unlock the following "What would Scheme print?" questions:
$ python ok -q combinations -u
scm> (- 10 4)
scm> (* 7 6)
scm> (+ 1 2 3 4)
scm> (/ 8 2 2)
scm> (quotient 29 5)
scm> (modulo 29 5)
scm> (= 1 3) ; Scheme uses '=' instead of '==' for comparison
scm> (< 1 3)
scm> (or 1 #t) ; or special form short circuits
scm> (and #t #f (/ 1 0))
scm> (not #t)
scm> (define x 3)
scm> x
scm> (define y (+ x 4))
scm> y
scm> (define x (lambda (y) (* y 2)))
scm> (x y)
scm> (if (not (print 1)) (print 2) (print 3))
scm> (* (if (> 3 2) 1 2) (+ 4 5))
scm> (define foo (lambda (x y z) (if x y z)))
scm> (foo 1 2 (print 'hi))
scm> ((lambda (a) (print 'a)) 100)
Required Problems
In this section, you are required to complete the problems below and submit your code to OJ website as instructed in lab00 to get your answer scored.
Remember, you can use ok to test your code:
$ python ok # test functions
$ python ok -q <function> # test single function
Problem 1: Over or Under (100pts)
Define a procedure over-or-under which takes in a number a and a number b and returns the following:
- -1 if
ais less thanb - 0 if
ais equal tob - 1 if
ais greater thanb
(define (over-or-under a b)
'YOUR-CODE-HERE
)
;;; Tests
; scm> (over-or-under 1 2)
; -1
; scm> (over-or-under 2 1)
; 1
; scm> (over-or-under 1 1)
; 0
Remember, you can test your implementation with ok:
$ python ok -q over-or-under
Problem 2: Make Adder (100 pts)
Write the procedure make-adder which takes in an initial number, n, and then returns a procedure. This returned procedure takes in a number x and returns the result of x + n.
Hint: To return a procedure, you can either return a lambda expression or define another nested procedure. Remember that Scheme will automatically return the last clause in your procedure.
(define (make-adder n)
'YOUR-CODE-HERE
)
;;; Tests
; scm> (define adder (make-adder 5))
; adder
; scm> (adder 8)
; 13
Problem 3: Compose (100 pts)
Write the procedure composed, which takes in procedures f and g and outputs a new procedure. This new procedure takes in a number x and outputs the result of calling f on g of x.
(define (composed f g)
'YOUR-CODE-HERE
)
;;; Tests
; scm> (define (add-one x) (+ x 1))
; add-one
; scm> (define (mul-two x) (* x 2))
; mul-two
; scm> (define mul-two-then-add-one (composed add-one mul-two))
; mul-two-then-add-one
; scm> (mul-two-then-add-one 2)
; 5
Problem 4: GCD (100 pts)
let's implement the gcd function that finds the greatest common divisor of two positive integers. The remainder function that computes the remainder of two positive integers is given. It takes two integers as inputs and returns an integer of solution. A Python version is provided in case you forget about how to compute gcd using Euclidean algorithm.
def gcd(a, b):
if b == 0:
return a
return gcd(b, a % b)
(define (remainder a b)
(- a (* b (quotient a b))))
(define (gcd a b)
'YOUR-CODE-HERE
)
;;; Tests
; (gcd 2 3)
; 1
; (gcd 16 12)
; 4
Problem 4: Make A List (100 pts)
In this problem you will create the list with the following box-and-pointer diagram:
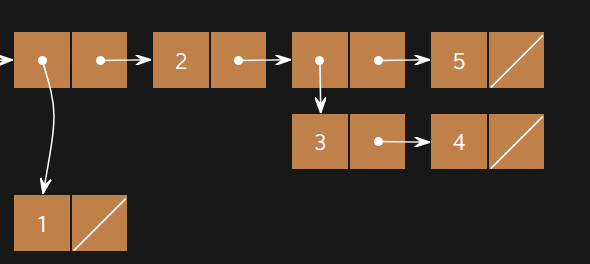
Challenge: try to create this list in multiple ways, and using multiple list constructors!
(define lst
'YOUR-CODE-HERE
)
Problem 5: Ordered (100 pts)
Implement a procedure called ordered, which takes a non-empty list of numbers and returns True if the numbers are in nondescending order, and False otherwise. Numbers are considered nondescending if each subsequent number is either larger or equal to the previous, that is:
1 2 3 3 4
Is nondescending, but:
1 2 3 3 2
Is not.
Hint: The built-in
null?function returns whether its argument isnil.
(define (ordered s)
'YOUR-CODE-HERE
)
;;; Tests
; scm> (ordered '(1 2 3 3 4))
; #t
; scm> (ordered '(1 2 3 3 2))
; #f