Instructions
Please download homework materials
hw07.zipfrom our QQ group if you don't have one.
In this homework, you are required to complete the problems described in section 2.
The starter code for these problems is provided in hw07.py.
Submission: As instructed before, you need to submit your work with Ok by python ok --submit.
You may submit more than once before the deadline,
and your score of this assignment will be the highest one of all your submissions.
Readings: You might find the following references to the textbook useful:
Required Problems
In this section, you are required to complete the problems below and submit your code to OJ website.
Remember, you can use ok to test your code:
$ python ok # test all classes and functions
$ python ok -q <class / function> # test single class / function
Problem 1: Polynomial (100pts)
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation of variables. An example of a polynomial of a single indeterminate \(x\) is \(x^2 − 4x + 7\).
We can use class Polynomial to represent polynomials, and a list of number to represent coefficients. For example, Polynomial([a_0, a_1, ..., a_n]) represents polynomial \(a_0 + a_1x + ... + a_nx^n\).
Implement required methods of class Polynomial such that representing a Polynomial object Polynomial([a_0, a_1, ..., a_n]) displays Polynomial([a_0, a_1, ..., a_n]), printing it displays a_0 + a_1*x^1 + ... + a_n*x^n and we can directly add or multiply two polynomial objects.
Note: the highest degree coefficient of a polynomial should not be 0, unless it is just \(0\).
Hint1: You can convert numbers to strings using the str function, and you can combine strings together using +.
Hint2: You may find python built-in function enumerate helpful.
class Polynomial:
"""Polynomial.
>>> a = Polynomial([0, 1, 2, 3, 4, 5, 0])
>>> a
Polynomial([0, 1, 2, 3, 4, 5])
>>> print(a)
0 + 1*x^1 + 2*x^2 + 3*x^3 + 4*x^4 + 5*x^5
>>> b = Polynomial([-1, 0, -2, 1, -3])
>>> print(b)
-1 + 0*x^1 + -2*x^2 + 1*x^3 + -3*x^4
>>> print(a + b)
-1 + 1*x^1 + 0*x^2 + 4*x^3 + 1*x^4 + 5*x^5
>>> print(a * b)
0 + -1*x^1 + -2*x^2 + -5*x^3 + -7*x^4 + -12*x^5 + -11*x^6 + -15*x^7 + -7*x^8 + -15*x^9
>>> print(a)
0 + 1*x^1 + 2*x^2 + 3*x^3 + 4*x^4 + 5*x^5
>>> print(b) # a and b should not be changed
-1 + 0*x^1 + -2*x^2 + 1*x^3 + -3*x^4
>>> zero = Polynomial([0])
>>> zero
Polynomial([0])
>>> print(zero)
0
"""
"*** YOUR CODE HERE ***"
You may find Python string formatting syntax or f-strings useful. A quick example:
>>> ten, twenty, thirty = 10, 'twenty', [30] >>> '{0} plus {1} is {2}'.format(ten, twenty, thirty) '10 plus twenty is [30]' >>> feeling = 'love' >>> course = 61 >>> f'I {feeling} {course}A!' 'I love 61A!'
Problem 2: Linked List (300pts in total)
The Link class is defined as below.
class Link:
"""A linked list.
>>> s = Link(1)
>>> s.first
1
>>> s.rest is Link.empty
True
>>> s = Link(2, Link(3, Link(4)))
>>> s.first = 5
>>> s.rest.first = 6
>>> s.rest.rest = Link.empty
>>> s # Displays the contents of repr(s)
Link(5, Link(6))
>>> s.rest = Link(7, Link(Link(8, Link(9))))
>>> s
Link(5, Link(7, Link(Link(8, Link(9)))))
>>> print(s) # Prints str(s)
<5 7 <8 9>>
"""
empty = ()
def __init__(self, first, rest=empty):
assert rest is Link.empty or isinstance(rest, Link)
self.first = first
self.rest = rest
def __repr__(self):
if self.rest is not Link.empty:
rest_repr = ', ' + repr(self.rest)
else:
rest_repr = ''
return 'Link(' + repr(self.first) + rest_repr + ')'
def __str__(self):
string = '<'
while self.rest is not Link.empty:
string += str(self.first) + ' '
self = self.rest
return string + str(self.first) + '>'
Problem 2.1: Remove Duplicates (100 pts)
Write a function that takes a sorted linked list of integers and mutates it so that all duplicates are removed.
Your implementation should mutate the original linked list. Do not create any new linked lists.
def remove_duplicates(lnk):
""" Remove all duplicates in a sorted linked list.
>>> lnk = Link(1, Link(1, Link(1, Link(1, Link(5)))))
>>> Link.__init__, hold = lambda *args: print("Do not steal chicken!"), Link.__init__
>>> try:
... remove_duplicates(lnk)
... finally:
... Link.__init__ = hold
>>> lnk
Link(1, Link(5))
"""
"*** YOUR CODE HERE ***"
Problem 2.2: Mutable Mapping (100 pts)
Implement deep_map_mut(fn, link), which applies a function fn onto all elements in the given linked list link. If an element is itself a non-empty linked list, apply fn to each of its elements, and so on.
Your implementation should mutate the original linked list. Do not create any new linked lists.
Hint: The built-in
isinstancefunction may be useful, but be careful aboutLink.empty.>>> s = Link(1, Link(2, Link(3, Link(4)))) >>> isinstance(s, Link) True >>> isinstance(s, int) False >>> isinstance(Link.empty, Link) False
def deep_map_mut(fn, link):
"""Mutates a deep link by replacing each item found with the
result of calling fn on the item. Does NOT create new Links (so
no use of Link's constructor)
Does not return the modified Link object.
>>> link1 = Link(3, Link(Link(4), Link(5, Link(6))))
>>> # Disallow the use of making new Links before calling deep_map_mut
>>> Link.__init__, hold = lambda *args: print("Do not steal chicken!"), Link.__init__
>>> try:
... deep_map_mut(lambda x: x * x, link1)
... finally:
... Link.__init__ = hold
>>> print(link1)
<9 <16> 25 36>
"""
"*** YOUR CODE HERE ***"
Problem 2.3: Reverse (100 pts)
Define reverse, which takes in a linked list and reverses the order of the links.
The function may not return a new list; it must mutate the original list. Return a
pointer to the head of the reversed list.
You may not just simply exchange the first to reverse the list. On the contrary, you should make change on rest.
There are at least three ways to solve this problem, can you come up with all?
def reverse(lnk):
""" Reverse a linked list.
>>> a = Link(1, Link(2, Link(3)))
>>> # Disallow the use of making new Links before calling reverse
>>> Link.__init__, hold = lambda *args: print("Do not steal chicken!"), Link.__init__
>>> try:
... r = reverse(a)
... finally:
... Link.__init__ = hold
>>> print(r)
<3 2 1>
>>> a.first # Make sure you do not change first
1
"""
"*** YOUR CODE HERE ***"
Problem 3: Tree (500pts in total)
The Tree class is defined as below.
class Tree:
"""
>>> t = Tree(3, [Tree(2, [Tree(5)]), Tree(4)])
>>> t.label
3
>>> t.branches[0].label
2
>>> t.branches[1].is_leaf()
True
"""
def __init__(self, label, branches=[]):
for b in branches:
assert isinstance(b, Tree)
self.label = label
self.branches = list(branches)
def is_leaf(self):
return not self.branches
def __repr__(self):
if self.branches:
branch_str = ', ' + repr(self.branches)
else:
branch_str = ''
return 'Tree({0}{1})'.format(self.label, branch_str)
def __str__(self):
def print_tree(t, indent=0):
tree_str = ' ' * indent + str(t.label) + "\n"
for b in t.branches:
tree_str += print_tree(b, indent + 1)
return tree_str
return print_tree(self).rstrip()
Problem 3.1: Equal Trees (100 pts)
Recall that when Python evaluates the expression a + b, it is in fact evaluating a.__add__(b). Similarly, when Python evaluates the expression a == b, it is in fact evaluating a.__eq__(b).
Implement spcial method __eq__ in class Tree, such that we can simply use t1 == t2 to judge whether two trees t1 and t2 are equivalent trees (i.e. have equivalent labels and equivalent branches).
Note: unlike problem 6.2 in midterm exam, this time we require two equivalent trees should have branches in the same order.
class Tree:
...
def __eq__(self): # Does this line need to be changed?
"""Returns whether two trees are equivalent.
>>> t1 = Tree(1, [Tree(2, [Tree(3), Tree(4)]), Tree(5, [Tree(6)]), Tree(7)])
>>> t1 == t1
True
>>> t2 = Tree(1, [Tree(2, [Tree(3), Tree(4)]), Tree(5, [Tree(6)]), Tree(7)])
>>> t1 == t2
True
>>> t3 = Tree(0, [Tree(2, [Tree(3), Tree(4)]), Tree(5, [Tree(6)]), Tree(7)])
>>> t4 = Tree(1, [Tree(5, [Tree(6)]), Tree(2, [Tree(3), Tree(4)]), Tree(7)])
>>> t5 = Tree(1, [Tree(2, [Tree(3), Tree(4)]), Tree(5, [Tree(6)])])
>>> t1 == t3 or t1 == t4 or t1 == t5
False
"""
"*** YOUR CODE HERE ***"
Problem 3.2: Generate Paths (100 pts)
Define a generator function generate_paths which takes in a Tree t, a value value, and returns a generator object which yields each path from the root of t to a node that has label value.
t is implemented with a class, not as the function-based ADT.
Each path should be represented as a list of the labels along that path in the tree. You may yield the paths in any order.
def generate_paths(t, value):
"""Yields all possible paths from the root of t to a node with the label value
as a list.
>>> t1 = Tree(1, [Tree(2, [Tree(3), Tree(4, [Tree(6)]), Tree(5)]), Tree(5)])
>>> print(t1)
1
2
3
4
6
5
5
>>> next(generate_paths(t1, 6))
[1, 2, 4, 6]
>>> path_to_5 = generate_paths(t1, 5)
>>> sorted(list(path_to_5))
[[1, 2, 5], [1, 5]]
>>> t2 = Tree(0, [Tree(2, [t1])])
>>> print(t2)
0
2
1
2
3
4
6
5
5
>>> path_to_2 = generate_paths(t2, 2)
>>> sorted(list(path_to_2))
[[0, 2], [0, 2, 1, 2]]
"""
"*** YOUR CODE HERE ***"
Problem 3.3: Iterator Tree Link Tree Iterator (100 pts)
Implement the function funcs, which is a generator that takes in a linked list link and yields functions.
The linked list link defines a path from the root of the tree to one of its nodes, with each element of link specifying which branch to take by index. Applying all functions sequentially to a Tree instance will evaluate to the label of the node at the end of the specified path.
For example, using the Tree t defined in the code, funcs(Link(2)) yields 2 functions. The first gets the third branch from t -- the branch at index 2 -- and the second function gets the label of this branch.
>>> func_generator = funcs(Link(2)) # get label of third branch
>>> f1 = next(func_generator)
>>> f2 = next(func_generator)
>>> f2(f1(t))
4
def funcs(link):
"""
>>> t = Tree(1, [Tree(2,
... [Tree(5),
... Tree(6, [Tree(8)])]),
... Tree(3),
... Tree(4, [Tree(7)])])
>>> print(t)
1
2
5
6
8
3
4
7
>>> func_generator = funcs(Link.empty) # get root label
>>> f1 = next(func_generator)
>>> f1(t)
1
>>> func_generator = funcs(Link(2)) # get label of third branch
>>> f1 = next(func_generator)
>>> f2 = next(func_generator)
>>> f2(f1(t))
4
>>> # This just puts the 4 values from the iterable into f1, f2, f3, f4
>>> f1, f2, f3, f4 = funcs(Link(0, Link(1, Link(0))))
>>> f4(f3(f2(f1(t))))
8
>>> f4(f2(f1(t)))
6
"""
"*** YOUR CODE HERE ***"
Problem 3.4: Count Coins Tree (100 pts)
You want to help your friend learn tree recursion. They don't quite understand all the recursive calls and how they work, so you decide to make a tree of recursive calls to showcase the tree in tree in tree recursion. You pick the count_coins problem.
Implement count_coins_tree, which takes in a non-negative integer n and returns a tree representing the recursive calls of count change.
Since you don't want your trees to get too big, you decide to only include the recursive calls that eventually lead to a valid way of making change.
See the code below for an implementation of count_coins.
def count_coins(change, denominations):
"""
Given a positive integer change, and a list of integers denominations,
a group of coins makes change for change if the sum of the values of
the coins is change and each coin is an element in denominations.
count_coins returns the number of such groups.
"""
if change == 0:
return 1
if change < 0:
return 0
if len(denominations) == 0:
return 0
without_current = count_coins(change, denominations[1:])
with_current = count_coins(change - denominations[0], denominations)
return without_current + with_current
For the times when either recursive call returns None, you don't want to include that in your branches when making the tree. If both recursive calls return None, then you want to return None.
Each leaf for the count_coins_tree(15, [1, 5, 10, 25]) tree is one of these groupings.
- 15 1-cent coins
- 10 1-cent, 1 5-cent coins
- 5 1-cent, 2 5-cent coins
- 5 1-cent, 1 10-cent coins
- 3 5-cent coins
- 1 5-cent, 1 10-cent coin
Note: the label of your tree should be string.
def count_coins_tree(change, denominations):
"""
>>> count_coins_tree(1, []) # Return None since no ways to make change wuth no denominations
>>> t = count_coins_tree(3, [1, 2])
>>> print(t) # 2 ways to make change for 3 cents
3, [1, 2]
2, [1, 2]
2, [2]
1
1, [1, 2]
1
>>> # The tree that shows the recursive calls that result
>>> # in the 6 ways to make change for 15 cents
>>> t = count_coins_tree(15, [1, 5, 10, 25])
>>> print(t)
15, [1, 5, 10, 25]
15, [5, 10, 25]
10, [5, 10, 25]
10, [10, 25]
1
5, [5, 10, 25]
1
14, [1, 5, 10, 25]
13, [1, 5, 10, 25]
12, [1, 5, 10, 25]
11, [1, 5, 10, 25]
10, [1, 5, 10, 25]
10, [5, 10, 25]
10, [10, 25]
1
5, [5, 10, 25]
1
9, [1, 5, 10, 25]
8, [1, 5, 10, 25]
7, [1, 5, 10, 25]
6, [1, 5, 10, 25]
5, [1, 5, 10, 25]
5, [5, 10, 25]
1
4, [1, 5, 10, 25]
3, [1, 5, 10, 25]
2, [1, 5, 10, 25]
1, [1, 5, 10, 25]
1
"""
"*** YOUR CODE HERE ***"
Problem 3.5: Decorate Christmas Tree (100 pts)
Christmas is coming soon. Isla bought a Christmas tree for Tsukasa. A Christmas tree is a Tree instance. There are some gifts on every nodes of the tree, and the label of each node is the number of gifts on it. Every gifts have the same weight.
We say a tree is balanced if it is a leaf or the total weight of every branches are the same and all its branches are balanced. For example, the left tree is balanced but the right one is not.
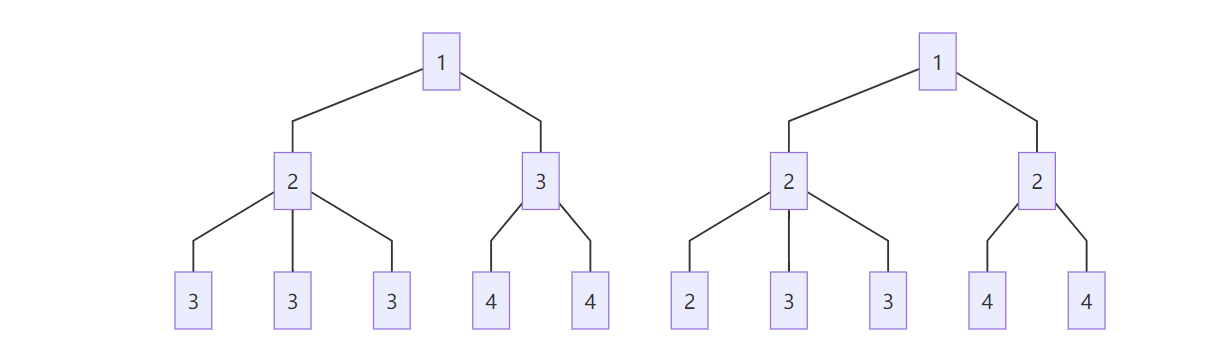
Isla wants to buy more gifts and hang them on the tree to balance it. Help her implement balance_tree, which takes in a tree and hangs gifts as few as possible on it to balance it.
Note: For trees which have more than one ways to balance with the same minimum number of gifts, you can choose any one and it won't influence your score.
def balance_tree(t):
"""Balance a tree.
>>> t1 = Tree(1, [Tree(2, [Tree(2), Tree(3), Tree(3)]), Tree(2, [Tree(4), Tree(4)])])
>>> balance_tree(t1)
>>> t1
Tree(1, [Tree(2, [Tree(3), Tree(3), Tree(3)]), Tree(3, [Tree(4), Tree(4)])])
"""
"*** YOUR CODE HERE ***"
Just for fun Problems
This section is out of scope for our course, so the problems below is optional. That is, the problems in this section don't count for your final score and don't have any deadline. Do it at any time if you want an extra challenge or some practice with higher order function and abstraction!
To check the correctness of your answer, you can submit your code to Contest 'Just for fun'.
Problem 4: Has Cycle (0pts)
The Link class can represent lists with cycles. That is, a list may contain itself as a sublist. Implement has_cycle that returns whether its argument, a Link instance, contains a cycle. Try to solve it with constant space! (i.e. no list, dict, set or any other container)
Hint: use two pointers.
def has_cycle(lnk):
""" Returns whether lnk has cycle.
>>> lnk = Link(1, Link(2, Link(3)))
>>> has_cycle(lnk)
False
>>> lnk.rest.rest.rest = lnk
>>> has_cycle(lnk)
True
>>> lnk.rest.rest.rest = lnk.rest
>>> has_cycle(lnk)
True
"""
"*** YOUR CODE HERE ***"
Problem 5: Decorate Christmas Tree II (0 pts)
This time, Isla bought 20 super big Christmas trees, which all have more than 100000 nodes! Can you still work out in less than 5 seconds?
Hint1: You should scan every node only constant times.
Hint2: You can set up new attribute of Tree instance in your solution to memorize something! It's not abstraction barrier violation!
Problem 6: Little Blue Whale Installs Camera (0 pts)
Given a tree, the little blue whale needs to install camera on the node of the tree. Each camera on a node can monitor its parent node, child nodes and itself. In order to be able to monitor all nodes of the tree, please implement install_camera, which calculates the minimum number of cameras that the little blue whale needs to install.
Note: the labels of nodes from input tree are all 0, and it's ok to modify it.
Hint: Use label to mark the node. For example, 0 for not monitored, 1 for camera, and 2 for monitored by camera in other node.
def install_camera(t):
"""Calculates the minimum number of cameras that need to be installed.
>>> t = Tree(0, [Tree(0, [Tree(0), Tree(0)])])
>>> install_camera(t)
1
>>> t = Tree(0, [Tree(0, [Tree(0, [Tree(0)])])])
>>> install_camera(t)
2
"""
"*** YOUR CODE HERE ***"