Project 4: Scheme Interpreter

splash

Eval calls apply, which just calls eval again! When does it all end?

Download Project Materials

To get started, download project materials project4.zip from our QQ group if you don't have one. Below is a list of all the files you will see in the project4.zip. You have to make changes to scheme/scheme.py, scheme/scheme_reader.py, and scheme/questions.scm in this project.

project4
  |-scheme
  |  |-scheme.py          # Implements the REPL and a evaluator for Scheme expressions
  |  |-scheme_reader.py   # Implements the reader for Scheme input. The Pair class and nil definition can be found here.
  |  |-scheme_tokens.py   # Implements the tokenizer for Scheme input
  |  |-scheme_builtins.py # Implements built-in Scheme procedures in Python
  |  |-buffer.py          # Implements the Buffer class, used in scheme_reader.py
  |  |-ucb.py             # Utility functions for use in 61A projects
  |  |-questions.scm      # Contains skeleton code for Phase III
  |  |-tests.scm          # Collection of test cases written in Scheme
  |  |-ok                 # The autograder
  |  |-submit.py          # The submission script (DO NOT MODIFY)
  |  |-tests              # A directory of tests used by ok
  |  `-mytests.rst        # A file where you can add your own tests
  `-project4.pdf          # Instructions for this project you must read

Introduction

Submission: This project has four phases. Phases 1, 2, and 3 are compulsory while Phase 4 is optional. You only need to submit your answers to the former three phases. When you are done, submit your code to our Grader server as instructed in lab07 by python submit.py --stuid <YOUR STUDENT ID> --stuname <YOUR NAME>. You may submit more than once before the deadline; grader will record the highest score graded from your submissions. Check that you have successfully submitted your code and what your score is on Grader website.

See lab07 for more instructions on on submitting assignments.

WARNING: Do not modify submit.py!

CS 61A has also provided a language specification and built-in procedure reference for the CS 61A subset of Scheme that you'll be building in this project. Reading the entirety of either of these documents should not be necessary, but we'll point out useful sections from the documentation in each part of the project.

In this project, you will develop an interpreter for a subset of the Scheme language. As you proceed, think about the issues that arise in the design of a programming language; many quirks of languages are byproducts of implementation decisions in interpreters and compilers. The subset of the language used in this project is described in the functional programming section of Composing Programs. Since we only include a subset of the language, your interpreter will not exactly match the behavior of other interpreters.

You will also implement some small programs in Scheme. Scheme is a simple but powerful functional language. You should find that much of what you have learned about Python transfers cleanly to Scheme as well as to other programming languages.

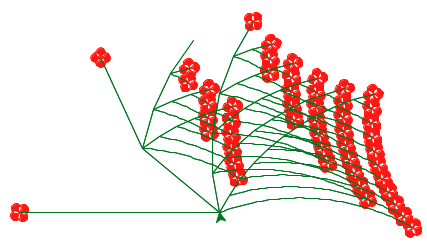
Later, there will also be an open-ended graphics contest (released separately) that challenges you to produce recursive images in only a few lines of Scheme. As an example, the picture above abstractly depicts all the ways of making change for $0.50 using U.S. currency. All flowers appear at the end of a branch with length 50. Small angles in a branch indicate an additional coin, while large angles indicate a new currency denomination. In the contest, you too will have the chance to unleash your inner recursive artist.

Suggestions

For the functions that we ask you to complete, there may be some initial code that we provide. If you would rather not use that code, feel free to delete it and start from scratch. You may also add new function definitions as you see fit.

However, please do not modify any other functions. Doing so may result in your code failing our framework. Also, please do not change any function signatures (names, argument order, or number of arguments).

Interpreter details

Scheme features

Read-Eval-Print. The interpreter reads Scheme expressions, evaluates them, and displays the results.

scm> 2
2
scm> (+ 2 3)
5
scm> ((lambda (x) (* x x)) 5)
25

The starter code for your Scheme interpreter in scheme.py can successfully evaluate the first expression above, since it consists of a single number. The second (a call to a built-in procedure) and the third (a computation of 5 squared) will not work just yet.

Load. You can load a file by passing in a symbol for the file name. For example, to load tests.scm, evaluate the following call expression.

scm> (load 'tests)

Symbols. Various dialects of Scheme are more or less permissive about identifiers (which serve as symbols and variable names).

Our rule is that:

An identifier is a sequence of letters (a-z and A-Z), digits, and characters in !$%&*/:<=>?@^_~-+. that do not form a valid integer or floating-point numeral and are not existing special form shorthands.

Our version of Scheme is case-insensitive: two identifiers are considered identical if they match except possibly in the capitalization of letters. They are internally represented and printed in lower case:

scm> 'Hello
hello

Turtle Graphics. In addition to standard Scheme procedures, we include procedure calls to the Python turtle package. This will come in handy for the contest.

You can read the turtle module documentation online.

Note: The turtle Python module may not be installed by default on your personal computer. However, the turtle module is installed on the instructional machines. So, if you wish to create turtle graphics for this project (i.e. for the contest), then you'll either need to setup turtle on your personal computer or use university computers.

Implementation overview

Here is a brief overview of each of the Read-Eval-Print Loop components in our interpreter. Refer to this section as you work through the project as a reminder of how all the small pieces fit together!

Exceptions. As you develop your Scheme interpreter, you may find that Python raises various uncaught exceptions when evaluating Scheme expressions. As a result, your Scheme interpreter will halt. Some of these may be the results of bugs in your program, but some might just be errors in user programs. The former should be fixed by debugging your interpreter and the latter should be handled, usually by raising a SchemeError. All SchemeError exceptions are handled and printed as error messages by the read_eval_print_loop function in scheme.py. Ideally, there should never be unhandled Python exceptions for any input to your interpreter.

Running the interpreter

To start an interactive Scheme interpreter session, type:

python scheme.py

You can use your Scheme interpreter to evaluate the expressions in an input file by passing the file name as a command-line argument to scheme.py:

python scheme.py tests.scm

Currently, your Scheme interpreter can handle a few simple expressions, such as:

scm> 1
1
scm> 42
42
scm> true
#t

To exit the Scheme interpreter, press Ctrl-d or evaluate the exit procedure (after completing problems 3 and 4):

scm> (exit)

Phase 1: The Reader

All changes in this part should be made in scheme_reader.py.

In Parts I and II, you will develop the interpreter in several stages:

The first part of this project deals with reading and parsing user input. Our reader will parse Scheme code into Python values with the following representations:

Input Example Scheme Expression Type Our Internal Representation
scm> 1 Numbers Python's built-in int and float values
scm> x Symbols Python's built-in string values
scm> #t Booleans (#t, #f) Python's built-in True, False values
scm> (+ 2 3) Combinations Instances of the Pair class, defined in scheme_reader.py
scm> nil nil The nil object, defined in scheme_reader.py

When we refer to combinations in this project, we are referring to both call expressions and special forms.

If you haven't already, make sure to read the Implementation overview section above to understand how the reader is broken up into parts.

In our implementation, we store tokens ready to be parsed in Buffer instances. For example, a buffer containing the input (+ (2 3)) would have the tokens '(', '+', '(', 2, 3, ')', and ')'. See the doctests in buffer.py for more examples. You do not have to understand the code in this file.

You will write the parsing functionality, which consists of two mutually recursive functions scheme_read and read_tail. These functions each take in a single parameter, src, which is an instance of Buffer.

There are two methods defined in buffer.py that you'll use to interact with src:

Note that you cannot index into the Buffer object (i.e. buffer[1] is not valid).

Problem 1 (200 pts)

First, implement scheme_read and read_tail so that they can parse combinations and atomic expressions. The expected behavior is as follows:

In short, scheme_read returns the next single complete expression in the buffer and read_tail returns the rest of a list or pair in the buffer. Both functions mutate the buffer, removing the tokens that have already been processed.

The behavior of both functions depends on the first token currently in src. They should be implemented as follows:

scheme_read:

read_tail:

For more hints and a start on how to approach this problem, take a look at this portion of lecture for additional skeleton code.

Before writing any code, test your understanding of the problem:

python ok --local -q 01 -u

After writing code, test your implementation:

python ok --local -q 01

Now that your parser is complete, you should test the read-eval-print loop by running python scheme_reader.py --repl. Every time you type in a value into the prompt, both the str and repr values of the parsed expression are printed. You can try the following inputs:

read> 42
str : 42
repr: 42
read> nil
str : ()
repr: nil
read> (1 (2 3) (4 (5)))
str : (1 (2 3) (4 (5)))
repr: Pair(1, Pair(Pair(2, Pair(3, nil)), Pair(Pair(4, Pair(Pair(5, nil), nil)), nil)))

To exit the interpreter, you can type exit.

Phase 2: The Evaluator

All changes in this part should only be made in scheme.py except Problem 6, where both scheme.py and scheme_reader.py should be changed.

In the starter implementation given to you, the evaluator can only evaluate self-evaluating expressions: numbers, booleans, and nil.

Read the first two sections of scheme.py, called Eval/Apply and Environments.

These are all of the essential components of the interpreter; the rest of scheme.py defines special forms and input/output behavior.

Test your understanding of how these components fit together by unlocking the tests for eval_apply.

python ok --local -q eval_apply -u

Some Core Functionality

Problem 2 (100 pts)

Implement the define and lookup methods of the Frame class. Each Frame object has the following instance attributes:

1) define takes a symbol (represented by a Python string) and a value and binds the value to that symbol in the frame.

2) lookup takes a symbol and returns the value bound to that name in the first Frame that the name is found in the current environment. Recall that an environment is defined as a frame, its parent frame, and all its ancestor frames, including the Global Frame. Therefore,

Before writing any code, test your understanding of the problem:

python ok --local -q 02 -u

After writing code, test your implementation:

python ok --local -q 02

After you complete this problem, you can open your Scheme interpreter (with python scheme.py). You should be able to look up built-in procedure names:

scm> +
#[+]
scm> odd?
#[odd?]
scm> display
#[display]

However, your Scheme interpreter will still not be able to call these procedures. Let's fix that.

Remember, at this point you can only exit the interpreter by pressing Ctrl-d.

Problem 3 (100 pts)

To be able to call built-in procedures, such as +, you need to complete the apply method in the class BuiltinProcedure. Built-in procedures are applied by calling a corresponding Python function that implements the procedure. For example, the + procedure in Scheme is implemented as the add function in Python.

To see a list of all Scheme built-in procedures used in the project, look in the scheme_builtins.py file. Any function decorated with @builtin will be added to the globally-defined BUILTINS list.

A BuiltinProcedure has two instance attributes:

The apply method of BuiltinProcedure takes a list of argument values and the current environment. Note that args is a Scheme list represented as a Pair object. Your implementation should do the following:

Before writing any code, test your understanding of the problem:

python ok --local -q 03 -u

After writing code, test your implementation:

python ok --local -q 03

Problem 4 (100 pts)

scheme_eval evaluates a Scheme expression, represented as a sequence of Pair objects, in a given environment. Most of scheme_eval has already been implemented for you. It currently looks up names in the current environment, returns self-evaluating expressions (like numbers) and evaluates special forms.

Implement the missing part of scheme_eval, which evaluates a call expression. To evaluate a call expression, we do the following:

  1. Evaluate the operator (which should evaluate to an instance of Procedure)
  2. Evaluate all of the operands
  3. Apply the procedure on the evaluated operands

You'll have to recursively call scheme_eval in the first two steps. Here are some other functions/methods you should use:

Note: Please do not mutate the passed in expr.

Before writing any code, test your understanding of the problem:

python ok --local -q 04 -u

After writing code, test your implementation:

python ok --local -q 04

Note: some of these tests call a primitive (built-in) procedure called print-then-return. This is a "dummy" procedure used only in this project, so you will not need to use it elsewhere. You will only ever come across it if you are failing those tests.

print-then-return takes in two arguments. It prints out its first argument and then returns its second.

Your interpreter should now be able to evaluate built-in procedure calls, giving you the functionality of the Calculator language and more.

scm> (+ 1 2)
3
scm> (* 3 4 (- 5 2) 1)
36
scm> (odd? 31)
#t

Problem 5 (100 pts)

Next, we'll implement defining names. Recall that the define special form in Scheme can be used to either assign a name to the value of a given expression or to create a procedure and bind it to a name:

scm> (define a (+ 2 3))  ; Binds the name a to the value of (+ 2 3)
a
scm> (define (foo x) x)  ; Creates a procedure and binds it to the name foo
foo

The type of the first operand tells us what is being defined:

Read the Scheme Specifications to understand the behavior of the define special form! This problem only provides the behavior for binding expressions, not procedures, to names.

There are two missing parts in the do_define_form function, which handles the (define ...) special forms. For this problem, implement just the first part, which evaluates the second operand to obtain a value and binds the first operand, a symbol, to that value. do_define_form should return the name after performing the binding.

scm> (define tau (* 2 3.1415926))
tau

Before writing any code, test your understanding of the problem:

python ok --local -q 05 -u

After writing code, test your implementation:

python ok --local -q 05

You should now be able to give names to values and evaluate the resulting symbols. Note that eval takes an expression represented as a list and evaluates it.

scm> (eval (define tau 6.28))
6.28
scm> (eval 'tau)
6.28
scm> tau
6.28
scm> (define x 15)
x
scm> (define y (* 2 x))
y
scm> y
30
scm> (+ y (* y 2) 1)
91
scm> (define x 20)
x
scm> x
20

Consider the following test:

(define x 0)
; expect x
((define x (+ x 1)) 2)
; expect Error
x
; expect 1

Here, an Error is raised because the operator does not evaluate to a procedure. However, if the operator is evaluated multiple times before raising an error, x will be bound to 2 instead of 1, causing the test to fail. Therefore, if your interpreter fails this test, you'll want to make sure you only evaluate the operator once in scheme_eval.

Problem 6 (100 pts)

To complete the core functionality, let's implement quoting in our interpreter. In Scheme, you can quote expressions in two ways: with the quote special form or with the symbol '. Recall that the quote special form returns its operand expression without evaluating it:

scm> (quote hello)
hello
scm> '(cons 1 2)  ; Equivalent to (quote (cons 1 2))
(cons 1 2)

Read the Scheme Specifications to understand the behavior of the quote special form.

Let's take care of the quote special form first. Implement the do_quote_form function so that it simply returns the unevaluated operand to the special form. After completing this function, you should be able to evaluate quoted expressions. Try out some of the following in your interpreter!

scm> (quote a)
a
scm> (quote (1 2))
(1 2)
scm> (quote (1 (2 three (4 5))))
(1 (2 three (4 5)))
scm> (car (quote (a b)))
a

Next, complete your implementation of scheme_read in scheme_reader.py by handling the case for '. First, notice that '<expr> translates to (quote <expr>). That means that we need to wrap the expression following ' (which you can get by recursively calling scheme_read) into the quote special form, which, like all special forms, is really just a list. For example, 'bagel should be represented as Pair('quote', Pair('bagel', nil)) For another example, '(1 2) should be represented as Pair('quote', Pair(Pair(1, Pair(2, nil)), nil)). After completing your scheme_read implementation, the following quoted expressions should now work as well.

scm> 'hello
hello
scm> '(1 2)
(1 2)
scm> '(1 (2 three (4 5)))
(1 (2 three (4 5)))
scm> (car '(a b))
a
scm> (eval (cons 'car '('(1 2))))
1

Before writing any code, test your understanding of the problem:

python ok --local -q 06 -u

After writing code, test your implementation:

python ok --local -q 06

At this point in the project, your Scheme interpreter should support the following features:

User-Defined Procedures

User-defined procedures are represented as instances of the LambdaProcedure class. A LambdaProcedure instance has three instance attributes:

Problem 7 (100 pts)

Read the Scheme Specifications to understand the behavior of the begin special form!

Change the eval_all function (which is called from do_begin_form) to complete the implementation of the begin special form. A begin expression is evaluated by evaluating all sub-expressions in order. The value of the begin expression is the value of the final sub-expression.

scm> (begin (+ 2 3) (+ 5 6))
11
scm> (define x (begin (display 3) (newline) (+ 2 3)))
3
x
scm> (+ x 3)
8
scm> (begin (print 3) '(+ 2 3))
3
(+ 2 3)

If eval_all is passed an empty list of expressions (nil), then it should return the Python value None, which represents the Scheme value undefined.

Before writing any code, test your understanding of the problem:

python ok --local -q 07 -u

After writing code, test your implementation:

python ok --local -q 07

Problem 8 (100 pts)

Read the Scheme Specifications to understand the behavior of the lambda special form!

A LambdaProcedure represents a user-defined procedure. It has a list of formals (parameter names), a body of expressions to evaluate, and a parent frame env.

Implement the do_lambda_form function, which creates and returns a LambdaProcedure instance. While you cannot call a user-defined procedure yet, you can verify that you have created the procedure correctly by typing a lambda expression into the interpreter prompt:

scm> (lambda (x y) (+ x y))
(lambda (x y) (+ x y))

In Scheme, it is legal to place more than one expression in the body of a procedure (there must be at least one expression). The body attribute of a LambdaProcedure instance is a Scheme list of body expressions.

Before writing any code, test your understanding of the problem:

python ok --local -q 08 -u

After writing code, test your implementation:

python ok --local -q 08

Problem 9 (100 pts)

Read the Scheme Specifications to understand the behavior of the define special form! In this problem, we'll finish defining the define form for procedures.

Currently, your Scheme interpreter is able to bind symbols to user-defined procedures in the following manner:

scm> (define f (lambda (x) (* x 2)))
f

However, we'd like to be able to use the shorthand form of defining named procedures:

scm> (define (f x) (* x 2))

Modify the do_define_form function so that it correctly handles the shorthand procedure definition form above. Make sure that it can handle multi-expression bodies.

Your implementation should do the following:

Before writing any code, test your understanding of the problem:

python ok --local -q 09 -u

After writing code, test your implementation:

python ok --local -q 09

You should now find that defined procedures evaluate to LambdaProcedure instances. However, you can't call them yet - we'll implement that in the next two problems.

scm> (define (square x) (* x x))
square
scm> square
(lambda (x) (* x x))

Problem 10 (100 pts)

Implement the make_child_frame method of the Frame class which will be used to create new call frames for user-defined procedures. This method takes in two arguments: formals, which is a Scheme list of symbols, and vals, which is a Scheme list of values. It should return a new child frame, binding the formal parameters to the values.

To do this:

Hint: The define method of a Frame instance creates a binding in that frame.

Before writing any code, test your understanding of the problem:

python ok --local -q 10 -u

After writing code, test your implementation:

python ok --local -q 10

Problem 11 (100 pts)

Implement the make_call_frame method in LambdaProcedure, which is needed by scheme_apply. It should create and return a new Frame instance using the make_child_frame method of the appropriate parent frame, binding formal parameters to argument values.

Since lambdas are lexically scoped, your new frame should be a child of the frame in which the lambda is defined. The env provided as an argument to make_call_frame is instead the frame in which the procedure is called, which will be useful if you implement dynamically scoped procedures in problem 18 (Optional).

Before writing any code, test your understanding of the problem:

python ok --local -q 11 -u

After writing code, test your implementation:

python ok --local -q 11

At this point in the project, your Scheme interpreter should support the following features:

Special Forms

Logical special forms include if, and, or, and cond. These expressions are special because not all of their sub-expressions may be evaluated.

In Scheme, only False is a false value. All other values (including 0 and nil) are true values. You can test whether a value is a true or false value using the provided Python functions is_true_primitive and is_false_primitive, defined in scheme_builtins.py.

Note: Scheme traditionally uses #f to indicate the false Boolean value. In our interpreter, that is equivalent to false or False. Similarly, true, True, and #t are all equivalent. However when unlocking tests, use #t and #f.

To get you started, we've provided an implementation of the if special form in the do_if_form function. Make sure you understand that implementation before starting the following questions.

Problem 12 (100 pts)

Read the Scheme Specifications to understand the behavior of the and and or special forms!

Implement do_and_form and do_or_form so that and and or expressions are evaluated correctly.

The logical forms and and or are short-circuiting. For and, your interpreter should evaluate each sub-expression from left to right, and if any of these evaluates to a false value, then #f is returned. Otherwise, it should return the value of the last sub-expression. If there are no sub-expressions in an and expression, it evaluates to #t.

scm> (and)
#t
scm> (and 4 5 6)  ; all operands are true values
6
scm> (and 4 5 (+ 3 3))
6
scm> (and #t #f 42 (/ 1 0))  ; short-circuiting behavior of and
#f

For or, evaluate each sub-expression from left to right. If any sub-expression evaluates to a true value, return that value. Otherwise, return #f. If there are no sub-expressions in an or expression, it evaluates to #f.

scm> (or)
#f
scm> (or 5 2 1)  ; 5 is a true value
5
scm> (or #f (- 1 1) 1)  ; 0 is a true value in Scheme
0
scm> (or 4 #t (/ 1 0))  ; short-circuiting behavior of or
4

Remember that you can use the provided Python functions is_true_primitive and is_false_primitive to test boolean values.

Before writing any code, test your understanding of the problem:

python ok --local -q 12 -u

After writing code, test your implementation:

python ok --local -q 12

Problem 13 (200 pts)

Read the Scheme Specifications to understand the behavior of the cond special form!

Fill in the missing parts of do_cond_form so that it returns the value of the first result sub-expression corresponding to a true predicate, or the result sub-expression corresponding to else. Some special cases:

Your implementation should match the following examples and the additional tests in tests.scm.

scm> (cond ((= 4 3) 'nope)
           ((= 4 4) 'hi)
           (else 'wait))
hi
scm> (cond ((= 4 3) 'wat)
           ((= 4 4))
           (else 'hm))
#t
scm> (cond ((= 4 4) 'here (+ 40 2))
           (else 'wat 0))
42

The value of a cond is undefined if there are no true predicates and no else. In such a case, do_cond_form should return None. If there is only an else, return its sub-expression. If it doesn't have one, return #t.

scm> (cond (False 1) (False 2))
scm> (cond (else))
#t

Before writing any code, test your understanding of the problem:

python ok --local -q 13 -u

After writing code, test your implementation:

python ok --local -q 13

Problem 14 (200 pts)

Read the Scheme Specifications to understand the behavior of the let special form!

The let special form binds symbols to values locally, giving them their initial values. For example:

scm> (define x 5)
x
scm> (define y 'bye)
y
scm> (let ((x 42)
           (y (* x 10)))  ; x refers to the global value of x, not 42
       (list x y))
(42 50)
scm> (list x y)
(5 bye)

Implement make_let_frame, which returns a child frame of env that binds the symbol in each element of bindings to the value of its corresponding expression. The bindings scheme list contains pairs that each contain a symbol and a corresponding expression.

You may find the following functions and methods useful:

Before writing any code, test your understanding of the problem:

python ok --local -q 14 -u

After writing code, test your implementation:

python ok --local -q 14

You can run the additional scheme tests to comprehensively test your implementation:

python ok --local -q tests.scm

Make sure to remove all of the (exit) commands, so that all the tests are run! We've provided 115 tests (not counting the optional tests), so if you don't see at least that many tests passed, you haven't removed all the (exit) commands.

Congratulations! Your Scheme interpreter implementation is now complete!

Phase 3: Write Some Scheme

Not only is your Scheme interpreter itself a tree-recursive program, but it is flexible enough to evaluate other recursive programs. Implement the following procedures in Scheme in the questions.scm file. In addition, for this part of the project, you may find the built-in procedure reference very helpful if you ever have a question about the behavior of a built-in Scheme procedure, like the difference between pair? and list?.

The autograder tests for the interpreter are not comprehensive, so you may have uncaught bugs in your implementation. Therefore, you may find it useful to test your code for these questions in the staff interpreter or the web editor and then try it in your own interpreter once you are confident your Scheme code is working.

Scheme Editor

As you're writing your code, you can debug using the Scheme Editor. In your scheme folder you will find a new editor. To run this editor, run python editor. This should pop up a window in your browser; if it does not, please navigate to localhost:31415 and you should see it.

Make sure to run python ok in a separate tab or window so that the editor keeps running.

Problem 15 (100 pts)

Implement the enumerate procedure, which takes in a list of values and returns a list of two-element lists, where the first element is the index of the value, and the second element is the value itself.

scm> (enumerate '(3 4 5 6))
((0 3) (1 4) (2 5) (3 6))
scm> (enumerate '())
()

Test your implementation before moving on:

python ok --local -q 15

Problem 16 (100 pts)

Implement the merge procedure, which takes in a comparator and two sorted list arguments and combines them into one sorted list. A comparator is a function that compares two values. Here, sorted means sorted according to the comparator. For example:

scm> (merge < '(1 4 6) '(2 5 8))
(1 2 4 5 6 8)
scm> (merge > '(6 4 1) '(8 5 2))
(8 6 5 4 2 1)

In case of a tie, you can choose to break the tie arbitrarily.

Test your implementation before moving on:

python ok --local -q 16

Problem 17 (200 pts)

Define a function nondecreaselist, which takes in a scheme list of numbers and outputs a list of lists, which overall has the same numbers in the same order, but grouped into lists that are non-decreasing.

For example, if the input is a list containing elements

(1 2 3 4 1 2 3 4 1 1 1 2 1 1 0 4 3 2 1)

the output should contain elements

((1 2 3 4) (1 2 3 4) (1 1 1 2) (1 1) (0 4) (3) (2) (1))

After writing code, test your implementation:

python ok --local -q 17

Phase 4: Optional

Problem 18 (0 pts)

Read the Scheme Specifications to understand the behavior of the mu special form!

All of the Scheme procedures we've seen so far use lexical scoping: the parent of the new call frame is the environment in which the procedure was defined. Another type of scoping, which is not standard in Scheme, is called dynamic scoping: the parent of the new call frame is the environment in which the procedure was evaluated. With dynamic scoping, calling the same procedure in different parts of your code can lead to different results (because of varying parent frames).

In this problem, we will implement the mu special form, a non-standard Scheme expression type representing a procedure that is dynamically scoped.

In the example below, we use the mu keyword instead of lambda to define a dynamically scoped procedure f:

scm> (define f (mu () (* a b)))
f
scm> (define g (lambda () (define a 4) (define b 5) (f)))
g
scm> (g)
20

The procedure f does not have an a or b defined; however, because f gets called within the procedure g, it has access to the a and b defined in g's frame.

Implement do_mu_form to evaluate the mu special form. A mu expression is similar to a lambda expression, but evaluates to a MuProcedure instance that is dynamically scoped. Most of the MuProcedure class has been provided for you.

In addition to filling out the body of do_mu_form, you'll need to complete the MuProcedure class so that when a call on such a procedure is executed, it is dynamically scoped. This means that when a MuProcedure created by a mu expression is called, the parent of the new call frame is the environment in which the call expression was evaluated. As a result, a MuProcedure does not need to store an environment as an instance attribute. It can refer to names in the environment from which it was called.

Looking at LambdaProcedure should give you a clue about what needs to be done to MuProcedure to complete it. You will not need to modify any existing methods, but may wish to implement new ones.

Before writing any code, test your understanding of the problem:

python ok --local -q 18 -u

After writing code, test your implementation:

python ok --local -q 18

Problem 19 (0 pts)

Complete the function optimize_tail_calls in scheme.py. It returns an alternative to scheme_eval that is properly tail recursive. That is, the interpreter will allow an unbounded number of active tail calls in constant space.

The Thunk class represents a thunk, an expression that needs to be evaluated in an environment. When scheme_optimized_eval receives a non-atomic expression in a tail context, then it returns an Thunk instance. Otherwise, it should repeatedly call original_scheme_eval until the result is a value, rather than a Thunk.

A successful implementation will require changes to several other functions, including some functions that we provided for you. All expressions throughout your interpreter that are in a tail context should be evaluated by calling scheme_eval with True as a third argument. Your goal is to determine which expressions are in a tail context throughout your code.

Once you finish, uncomment the following line in scheme.py to use your implementation:

scheme_eval = optimize_tail_calls(scheme_eval)

Test your implementation before moving on:

python ok --local -q 19

Problem 20 (0 pts)

Macros allow the language itself to be extended by the user. Simple macros can be provided with the define-macro special form. This must be used like a procedure definition, and it creates a procedure just like define. However, this procedure has a special evaluation rule: it is applied to its arguments without first evaluating them. Then the result of this application is evaluated.

This final evaluation step takes place in the caller's frame, as if the return value from the macro was literally pasted into the code in place of the macro.

Here is a simple example:

scm> (define (map f lst) (if (null? lst) nil (cons (f (car lst)) (map f (cdr lst)))))
scm> (define-macro (for formal iterable body)
....     (list 'map (list 'lambda (list formal) body) iterable))
scm> (for i '(1 2 3)
....     (print (* i i)))
1
4
9
(None None None)

The code above defines a macro for that acts as a map except that it doesn't need a lambda around the body.

In order to implement define-macro, implement complete the implementation for do_define_macro, which should create a MacroProcedure and bind it to the given name as in do_define_form. Then, update scheme_eval so that calls to macro procedures are evaluated correctly.

Hint: Use the apply_macro method in the MacroProcedure class to apply a macro to the operands in its call expression. This procedure is written to interact well with tail call optimization.

Test your implementation before moving on:

python ok --local -q 20

Conclusion

Congratulations! You have just implemented an interpreter for an entire language! If you enjoyed this project and want to extend it further, you may be interested in looking at more advanced features, like let* and letrec, unquote splicing, error tracing, and continuations.