Please download lab materials
lab06.zipfrom our QQ group if you don't have one.
In this lab, you have one task:
lab06.py, which is distributed as part of the lab materials in the code directory.Submission: As instructed above, you just need to submit your answer for problems described in section 3 to our OJ website. You may submit more than once before the deadline; only the final submission will be scored. See lab00 for more instructions on submitting assignments.
Readings: You might find the following reference to the textbook useful:
In this section, you need to think about what python would display if the code below were input to a python interpreter.
Read over the Link class in lab06.py. Make sure you understand the doctests.
To check the correctness of your answer, you can start a python interpreter, input the code into it, and compare the output displayed in the terminal with yours. It is ok for the interpreter to output nothing or raise an error.
>>> link = Link(1000)
>>> link.first
______
>>> link.rest is Link.empty
______
>>> link = Link(1000, 2000)
______
>>> link = Link(1000, Link())
______
>>> link = Link(1, Link(2, Link(3)))
>>> link.first
______
>>> link.rest.first
______
>>> link.rest.rest.rest is Link.empty
______
>>> link.first = 9001
>>> link.first
______
>>> link.rest = link.rest.rest
>>> link.rest.first
______
>>> link = Link(1)
>>> link.rest = link
>>> link.rest.rest.rest.rest.first
______
>>> link = Link(2, Link(3, Link(4)))
>>> link2 = Link(1, link)
>>> link2.first
______
>>> link2.rest.first
______
>>> link = Link(5, Link(6, Link(7)))
>>> link # Look at the __repr__ method of Link
______
>>> print(link) # Look at the __str__ method of Link
______
In this section, you are required to complete the problems below and submit your code to Contest lab06 in our OJ website as instructed in lab00 to get your answer scored.
Complete the Mint and Coin classes so that the coins created by a mint have the correct year and worth.
Mint instance has a year stamp. The update method sets the year stamp to the current_year class attribute of the Mint class.create method takes a subclass of Coin and returns an instance of that class stamped with the mint's year (which may be different from Mint.current_year if it has not been updated.)Coin's worth method returns the cents value of the coin plus one extra cent for each year of age beyond 50. A coin's age can be determined by subtracting the coin's year from the current_year class attribute of the Mint class.class Mint:
"""A mint creates coins by stamping on years.
The update method sets the mint's stamp to Mint.current_year.
>>> mint = Mint()
>>> mint.year
2020
>>> dime = mint.create(Dime)
>>> dime.year
2020
>>> Mint.current_year = 2100 # Time passes
>>> nickel = mint.create(Nickel)
>>> nickel.year # The mint has not updated its stamp yet
2020
>>> nickel.worth() # 5 cents + (80 - 50 years)
35
>>> mint.update() # The mint's year is updated to 2100
>>> Mint.current_year = 2175 # More time passes
>>> mint.create(Dime).worth() # 10 cents + (75 - 50 years)
35
>>> Mint().create(Dime).worth() # A new mint has the current year
10
>>> dime.worth() # 10 cents + (155 - 50 years)
115
>>> Dime.cents = 20 # Upgrade all dimes!
>>> dime.worth() # 20 cents + (155 - 50 years)
125
"""
current_year = 2020
def __init__(self):
self.update()
def create(self, kind):
"*** YOUR CODE HERE ***"
def update(self):
"*** YOUR CODE HERE ***"
class Coin:
def __init__(self, year):
self.year = year
def worth(self):
"*** YOUR CODE HERE ***"
class Nickel(Coin):
cents = 5
class Dime(Coin):
cents = 10
Write a function link_to_list that takes in a linked list and returns the sequence as a Python list. You may assume that the input list is shallow; none of the elements is another linked list.
Try to find both an iterative and recursive solution for this problem!
def link_to_list(link):
"""Takes a linked list and returns a Python list with the same elements.
>>> link = Link(1, Link(2, Link(3, Link(4))))
>>> link_to_list(link)
[1, 2, 3, 4]
>>> link_to_list(Link.empty)
[]
"""
"*** YOUR CODE HERE ***"
Write a function store_digits that takes in an integer n and returns a linked list where each element of the list is a digit of n.
def store_digits(n):
"""Stores the digits of a positive number n in a linked list.
>>> s = store_digits(1)
>>> s
Link(1)
>>> store_digits(2345)
Link(2, Link(3, Link(4, Link(5))))
>>> store_digits(876)
Link(8, Link(7, Link(6)))
"""
"*** YOUR CODE HERE ***"
Write a function cumulative_mul that mutates the Tree t so that each node's label becomes the product of all labels in the subtree rooted at the node.
def cumulative_mul(t):
"""Mutates t so that each node's label becomes the product of all labels in
the corresponding subtree rooted at t.
>>> t = Tree(1, [Tree(3, [Tree(5)]), Tree(7)])
>>> cumulative_mul(t)
>>> t
Tree(105, [Tree(15, [Tree(5)]), Tree(7)])
"""
"*** YOUR CODE HERE ***"
Define a generator function generate_paths which takes in a Tree t, a value value, and returns a generator object which yields each path from the root of t to a node that has label value.
t is implemented with a class, not as the function-based ADT.
Each path should be represented as a list of the labels along that path in the tree. You may yield the paths in any order.
We have provided a (partial) skeleton for you. You do not need to use this skeleton, but if your implementation diverges significantly from it, you might want to think about how you can get it to fit the skeleton.
def generate_paths(t, value):
"""Yields all possible paths from the root of t to a node with the label value
as a list.
>>> t1 = Tree(1, [Tree(2, [Tree(3), Tree(4, [Tree(6)]), Tree(5)]), Tree(5)])
>>> print(t1)
1
2
3
4
6
5
5
>>> next(generate_paths(t1, 6))
[1, 2, 4, 6]
>>> path_to_5 = generate_paths(t1, 5)
>>> sorted(list(path_to_5))
[[1, 2, 5], [1, 5]]
>>> t2 = Tree(0, [Tree(2, [t1])])
>>> print(t2)
0
2
1
2
3
4
6
5
5
>>> path_to_2 = generate_paths(t2, 2)
>>> sorted(list(path_to_2))
[[0, 2], [0, 2, 1, 2]]
"""
"*** YOUR CODE HERE ***"
for _______________ in _________________:
for _______________ in _________________:
"*** YOUR CODE HERE ***"
Hint: If you're having trouble getting started, think about how you'd approach this problem if it wasn't a generator function. What would your recursive calls be? With a generator function, what happens if you make a "recursive call" within its body?
The problems below may be a bit difficult. Therefore, we just assign 100 points for each so that you will not lose much scores if you failed to solve them. Take your time to overcome them.
Implement deep_map, which takes a function f and a link. It returns a new linked list with the same structure as link, but with f applied to any element within link or any Link instance contained in link.
The deep_map function should recursively apply fn to each of that Link's elements rather than to that Link itself.
Hint: You may find the built-in isinstance function useful. You can also use the type(link) == Link to check whether an object is a linked list.
def deep_map(f, link):
"""Return a Link with the same structure as link but with fn mapped over
its elements. If an element is an instance of a linked list, recursively
apply f inside that linked list as well.
>>> s = Link(1, Link(Link(2, Link(3)), Link(4)))
>>> print(deep_map(lambda x: x * x, s))
<1 <4 9> 16>
>>> print(s) # unchanged
<1 <2 3> 4>
>>> print(deep_map(lambda x: 2 * x, Link(s, Link(Link(Link(5))))))
<<2 <4 6> 8> <<10>>>
"""
"*** YOUR CODE HERE ***"
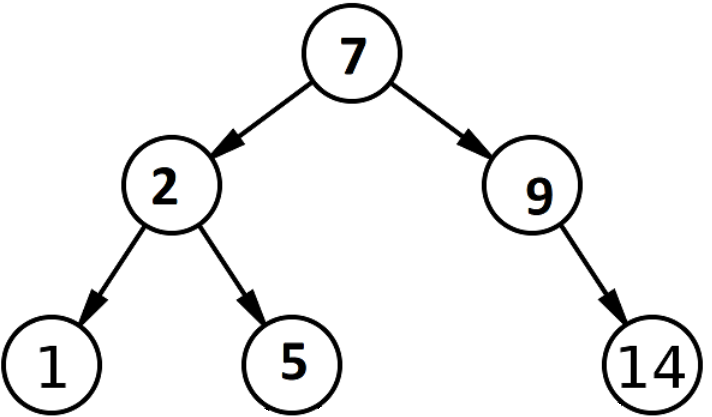
Write a function is_bst, which takes a Tree t and returns True if, and only if, t is a valid binary search tree, which means that:
An example of a BST is:

Note that, if a node has only one child, that child could be considered either the left or right child. You should take this into consideration.
Hint: It may be helpful to write helper functions bst_min and bst_max that return the minimum and maximum, respectively, of a Tree if it is a valid binary search tree.
def is_bst(t):
"""Returns True if the Tree t has the structure of a valid BST.
>>> t1 = Tree(6, [Tree(2, [Tree(1), Tree(4)]), Tree(7, [Tree(7), Tree(8)])])
>>> is_bst(t1)
True
>>> t2 = Tree(8, [Tree(2, [Tree(9), Tree(1)]), Tree(3, [Tree(6)]), Tree(5)])
>>> is_bst(t2)
False
>>> t3 = Tree(6, [Tree(2, [Tree(4), Tree(1)]), Tree(7, [Tree(7), Tree(8)])])
>>> is_bst(t3)
False
>>> t4 = Tree(1, [Tree(2, [Tree(3, [Tree(4)])])])
>>> is_bst(t4)
True
>>> t5 = Tree(1, [Tree(0, [Tree(-1, [Tree(-2)])])])
>>> is_bst(t5)
True
>>> t6 = Tree(1, [Tree(4, [Tree(2, [Tree(3)])])])
>>> is_bst(t6)
True
>>> t7 = Tree(2, [Tree(1, [Tree(5)]), Tree(4)])
>>> is_bst(t7)
False
"""
"*** YOUR CODE HERE ***"