Please download lab materials
lab03.zipfrom our QQ group if you don't have one.
In this lab, you have one task:
lab03.py, which is distributed as part of the lab materials in the code directory.Submission: As instructed above, you just need to submit your answer for problems described in section 3 to our OJ website. You may submit more than once before the deadline; only the final submission will be scored. See lab00 for more instructions on submitting assignments.
Readings: You might find the following reference to the textbook useful:
A recursive function is a function that calls itself in its body, either directly or indirectly. Recursive functions have three important components:
Let's look at the canonical example, factorial.
Factorial, denoted with the ! operator, is defined as:
For example,
5! = 5 * 4 * 3 * 2 * 1 = 120.
The recursive implementation for factorial is as follows:
def factorial(n):
if n == 0:
return 1
return n * factorial(n - 1)
We know from its definition that 0! is 1. Since n == 0 is the smallest number we can compute the factorial of, we use it as our base case. The recursive step also follows from the definition of factorial, i.e., n! = n * (n-1)!.
The next few questions in lab will have you writing recursive functions. Here are some general tips:
A tree recursive function is a recursive function that makes more than one call to itself, resulting in a tree-like series of calls.
A classic example of a tree recursion function is finding the nth Fibonacci number:
def fib(n):
if n == 0 or n == 1:
return n
return fib(n - 1) + fib(n - 2)
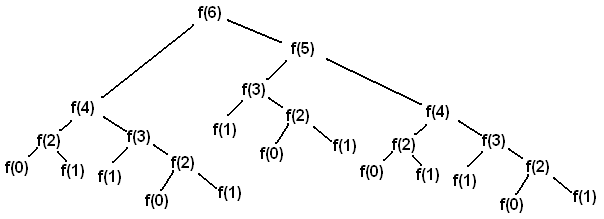
Calling fib(6) results in the following call structure (where f is fib):

Each f(i) node represents a recursive call to fib. Each recursive call makes another two recursive calls. f(0) and f(1) do not make any recursive calls because they are the base cases of the function. Because of these base cases, we are able to terminate the recursion and beginning accumulating the values.
Generally, tree recursion is effective when you want to explore multiple possibilities or choices at a single step. In these types of problems, you make a recursive call for each choice or for a group of choices. Here are some examples:
In this section, you are required to complete the problems below and submit your code to Contest lab03 in our OJ website as instructed in lab00 to get your answer scored.
Write a recursive function skip_add that takes a single argument n and returns n + n-2 + n-4 + n-6 + ... + 0. Assume n is non-negative.
this_file = __file__
def skip_add(n):
""" Takes a number n and returns n + n-2 + n-4 + n-6 + ... + 0.
>>> skip_add(5) # 5 + 3 + 1 + 0
9
>>> skip_add(10) # 10 + 8 + 6 + 4 + 2 + 0
30
>>> # Do not use while/for loops!
>>> from construct_check import check
>>> # ban iteration
>>> check(this_file, 'skip_add',
... ['While', 'For'])
True
"""
"*** YOUR CODE HERE ***"
You can use doctest to test your code:
$ python -m doctest lab03.py
Now, write a recursive implementation of summation, which takes a positive integer n and a function term. It applies term to every number from 1 to n including n and returns the sum of the results.
def summation(n, term):
"""Return the sum of the first n terms in the sequence defined by term.
Implement using recursion!
>>> summation(5, lambda x: x * x * x) # 1^3 + 2^3 + 3^3 + 4^3 + 5^3
225
>>> summation(9, lambda x: x + 1) # 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
54
>>> summation(5, lambda x: 2**x) # 2^1 + 2^2 + 2^3 + 2^4 + 2^5
62
>>> # Do not use while/for loops!
>>> from construct_check import check
>>> # ban iteration
>>> check(this_file, 'summation',
... ['While', 'For'])
True
"""
assert n >= 1
"*** YOUR CODE HERE ***"
The greatest common divisor of two positive integers a and b is the largest integer which evenly divides both numbers (with no remainder). Euclid, a Greek mathematician in 300 B.C., realized that the greatest common divisor of a and b is one of the following:
In other words, if a is greater than b and a is not divisible by b, then
gcd(a, b) = gcd(b, a % b)
Write the gcd function recursively using Euclid's algorithm.
def gcd(a, b):
"""Returns the greatest common divisor of a and b.
Should be implemented using recursion.
>>> gcd(34, 19)
1
>>> gcd(39, 91)
13
>>> gcd(20, 30)
10
>>> gcd(40, 40)
40
"""
"*** YOUR CODE HERE ***"
Consider an insect in an M by N grid. The insect starts at the bottom left corner, (0, 0), and wants to end up at the top right corner, (M-1, N-1). The insect is only capable of moving right or up. Write a function paths that takes a grid length and width and returns the number of different paths the insect can take from the start to the goal. (There is a closed-form solution to this problem, but try to answer it procedurally using recursion.)
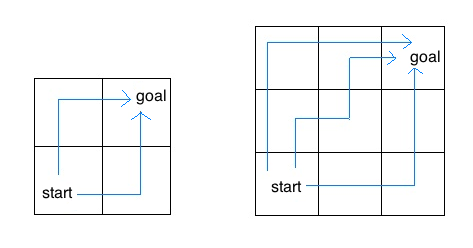
For example, the 2 by 2 grid has a total of two ways for the insect to move from the start to the goal. For the 3 by 3 grid, the insect has 6 different paths (only 3 are shown above).
def paths(m, n):
"""Return the number of paths from one corner of an
M by N grid to the opposite corner.
>>> paths(2, 2)
2
>>> paths(5, 7)
210
>>> paths(117, 1)
1
>>> paths(1, 157)
1
"""
"*** YOUR CODE HERE ***"
A subsequence of a number is a series of (not necessarily contiguous) digits of the number. For example, 12345 has subsequences that include 123, 234, 124, 245, etc. Your task is to get the maximum subsequence below a certain length.
def max_subseq(n, l):
"""
Return the maximum subsequence of length at most l that can be found in the given number n.
For example, for n = 20125 and l = 3, we have that the subsequences are
2
0
1
2
5
20
21
22
25
01
02
05
12
15
25
201
202
205
212
215
225
012
015
025
125
and of these, the maximum number is 225, so our answer is 225.
>>> max_subseq(20125, 3)
225
>>> max_subseq(20125, 5)
20125
>>> max_subseq(20125, 6) # note that 20125 == 020125
20125
>>> max_subseq(12345, 3)
345
>>> max_subseq(12345, 0) # 0 is of length 0
0
>>> max_subseq(12345, 1)
5
"""
"*** YOUR CODE HERE ***"
There are two key insights for this problem:
l since we used the last digit, and in the case where it isn't, we do not.d to the end of a number n is 10 * n + d.